UP | HOME

Graphs basics

1 The basics

Some concepts related to graphs:

  1. path
  2. cycle
  3. self loop
  4. directed graph
  5. simple digraph
  6. non-directed graph
  7. unconnected graph
  8. strongly connected graph
  9. Directed acyclic graph
  10. Ways to represent a graph
  11. articulation points
  12. Edges
  13. Vertex
  14. spanning trees

The definition of a graph:

\(G=(E,V)\)

So a graph is a set of pairs of edges and vertices. Time complexity for traversing a graph depends on the method you use. In this case it is O(n2) because we are representing the graph on a matrix. If we would use a linked list to represent it, it would take O(n).

2 traversing a non cyclic graph with bfs

  1. Visiting Visiting in this case means print the value.
  2. Exploring This means, visit all the adjacent nodes.

Below we have a simple undirected graph with its adjacent matrix table representation:

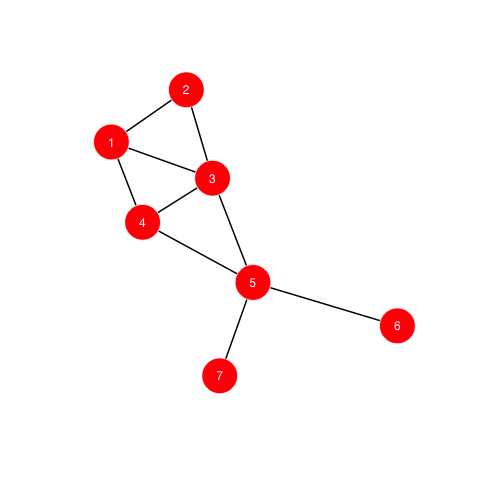
graph-1.png
Table 1: adjacent matrix: represents "am" variable on the snippets below.
  0 1 2 3 4 5 6 7
0 0 0 0 0 0 0 0 0
1 0 0 1 1 1 0 0 0
2 0 1 0 1 0 0 0 0
3 0 1 1 0 1 1 0 0
4 0 1 0 1 0 1 0 0
5 0 0 0 1 1 0 1 1
6 0 0 0 0 0 1 0 0
7 0 0 0 0 0 1 0 0 
#include "stdio.h"
#include "queue"
#include "stdlib.h"
#define N 8

using namespace std;

void bfs(int firstElement);

int main(int argc, char *argv[])
{
  printf("%s\n", "bfs with node: ");
  for (int i = 1; i < N; ++i) {
    printf("%d -> ", i);
    bfs(i);
    printf("\n");
  }

  return 0;
}

void bfs(int firstElement) {

  int * visited = (int *) malloc(sizeof(int) * N);
  queue<int> q;

  // initialize visited array
  for (int i = 0; i < N; i++)
    visited[i] = 0;

  // visit 
  printf("%d ", firstElement);

  // mark as visited
  visited[firstElement] = 1;
  // push to the queue
  q.push(firstElement);

  // repeat above process
  while (!q.empty()) {
    int r = q.front(); q.pop();

    for (int c = 1; c < N; c++)
      if (gam[r][c] == 1 && visited[c] == 0) {
        printf("%d ", c);
        q.push(c);
        visited[c] = 1;
      }
  }

  free(visited);
}

// Note: gam is the graph-adjacent-matrix
// the variable is loaded from the table displayed above

bfs with node: 
1 -> 1 2 3 4 5 6 7 
2 -> 2 1 3 4 5 6 7 
3 -> 3 1 2 4 5 6 7 
4 -> 4 1 3 5 2 6 7 
5 -> 5 3 4 6 7 1 2 
6 -> 6 5 3 4 7 1 2 
7 -> 7 5 3 4 6 1 2

3 DONE traversing non cyclic graph with dfs

#include <cstdio>
#include<stdio.h>
#include "stdlib.h"
#include "stack"
#define N 8

void dfs(int firstNode);
void recursive_dfs(int firstNode);
int *visited_nodes = (int *)malloc(sizeof(int) * N);
void clear_visited_nodes_array(void);

int main(int argc, char *argv[])
{

  // initialize global array
  for (int i = 0; i < N; ++i)
    visited_nodes[i] = 0;

  for (int i = 1; i < N; ++i) {
    printf("dfs for node:  %d -> ", i);
    recursive_dfs(i);
    printf("\n");
    clear_visited_nodes_array();
  }

  return 0;
}

void clear_visited_nodes_array() {
  for (int i = 0; i < N; ++i)
    visited_nodes[i] = 0;
}

void dfs(int firstElement) {
  // visit
  // explore
  int * visited = (int *) malloc(sizeof(int) * N);
  for (int i = 0; i < N; ++i)
    visited[i] = 0;

  std::stack<int> stack;

  // exploring
  stack.push(firstElement);

  while (!stack.empty()) {
    int e = stack.top(); stack.pop();

    if (visited[e])
      continue;

    printf("%d ", e);
    visited[e] = 1;
    for (int c = 1; c < N; c++)
      if (gam[e][c] == 1)
        stack.push(c);
  }
}

void recursive_dfs(int node) {
  if (visited_nodes[node] == 0) {
    printf("%d ", node);
    visited_nodes[node] = 1;
    for (int i = 1; i < N; ++i)
      if (gam[node][i] == 1 && visited_nodes[i] == 0) 
        recursive_dfs(i);
  }
}

dfs for node:  1 -> 1 2 3 4 5 6 7 
dfs for node:  2 -> 2 1 3 4 5 6 7 
dfs for node:  3 -> 3 1 2 4 5 6 7 
dfs for node:  4 -> 4 1 2 3 5 6 7 
dfs for node:  5 -> 5 3 1 2 4 6 7 
dfs for node:  6 -> 6 5 3 1 2 4 7 
dfs for node:  7 -> 7 5 3 1 2 4 6

4 Spanning trees

5 References

Some useful links that I used to build this entry.