Data Structures and C/C++ Graphs basics
1. Introduction
I am trying to practicing again the main concepts in programming with the help of one course about the main of data structures and algorithms. This course can be found in udemy.
So this file will be and is my playground for taking notes.
2. Let's started
All chapters will be in C or C++. This because, I am trying to remember the fundamentals, and C and C++ are almost the same, considered as low programming languages. We can look at conceptos like pointers, memory allocation, etc. Concepts that may not be to close for the end user on other programming languges of high level.
2.1. Pointers
So a pointer is simply a variable of 8 bytes (on 64 bit computer) or 4 bytes (on a 32 bit computer) that points to a memory address.
For instance, all beginner programmer will know a primitive type like int, which referers to integer. Usually an int type consists of 4 bytes (that means, 8 bits), in memory terms this means that to represent a integer value, the computer must reserve 4 bytes of memory on the main memory of the computer for the program on execution be able to run, use or represent an integer value.
That spot of reserved memory contains an address as a house contains an address. That means we can look for the address, to later get whatever the address holds.
Below there is a little C program that uses pointers.
#include <iostream> #define size 5 using namespace std; int main(int argc, char *argv[]) { // declare an array of 5 integers int array[size] = {1, 2, 3, 4, 5}; // declare pointer that points to an integer data type int *p; for (int i = 0; i < size; ++i) cout << array[i] << " "; cout << endl; // point to the above array // this can be done, because an array is a data structure // that reserves contiguous memory on the process/program timeline execution. p = array; for (int i = 0; i < size; ++i) cout << "value:" << p[i] << " memory address: " << &p[i] << endl; // same output . different way for (int i = 0; i < size; ++i) cout << "value:" << (*(p + i)) << " memory address: " << (p + i) << endl; // now lets change the value of an integer getting its reference and modifying the value int valuex = 10; cout << "valuex before: " << valuex << endl; int* xptr = &valuex; // the amperson indicates: "give me the memory adress of this variable" *xptr = 7; cout << "valuex after: " << valuex << endl; // Notes: // all the pointers occupy the same amount of memory. // the size of the pointer will depend on the system architecture target compile. // we can point to any existing type of data, that includes "structs". // pointers are used everywhere, in all programming languages, implicitly or explicitly but everywhere. return 0; }
1 2 3 4 5 value:1 memory address: 0x16efab4f0 value:2 memory address: 0x16efab4f4 value:3 memory address: 0x16efab4f8 value:4 memory address: 0x16efab4fc value:5 memory address: 0x16efab500 value:1 memory address: 0x16efab4f0 value:2 memory address: 0x16efab4f4 value:3 memory address: 0x16efab4f8 value:4 memory address: 0x16efab4fc value:5 memory address: 0x16efab500 valuex before: 10 valuex after: 7
#include <iostream> struct Book { float price; char name[50]; }; int main(int argc, char *argv[]) { Book bookx; // set up some random values strcpy(bookx.name, "C Programming"); bookx.price = 77; // declare a pointer to an struct struct Book * bookPtr; bookPtr = &bookx; std::cout << "Book Name: " << bookPtr->name << " Book price($dlls): " << bookPtr->price << std::endl; // changing the value by reference strcpy(bookPtr->name, "C++ Programming"); bookPtr->price = 87; std::cout << "Book Name: " << bookPtr->name << " Book price($dlls): " << bookPtr->price << std::endl; return 0; }
2.2. Allocating dynamic memory
To a program be able to start, it needs to be attached to a process, which the operating system needs to handle. This process asks the operating system for an amount of memory to be used by the program itself. One concept to know here is the stack memory*, and the *heap.
Below there is a simply sample of allocating dinamyc memory in C and C++.
#include<stdlib.h> #include<stdio.h> int main(int argc, char *argv[]) { // allocating memory using malloc helper function int* array = malloc(sizeof(int) * 5); array[0] = 7; printf("%d", array[0]); // Note: be aware that in C and C++ always you do memory allocation // you must free or release it when you finish to use it, // otherwise you can have memory leak problems. // In C we use the free function to release the allocated memory. // In C++ we use the delete keyword. (Look at the next c++ example snippet) free(array); return 0; }
7
#include <iostream> #include <ostream> int main(int argc, char *argv[]) { int *array = new int[5]; array[0] = 7; std::cout << array[0] << std::endl; // Notes: // instead of using malloc function as in C, we can use the 'new' keyword. // here we use the 'delete' keyword followed by the brackets to indicate that // we cant to release the allocated memory. delete [] array; return 0; }
7
3. Graphs
3.1. The basics
Some concepts related to graphs:
- path
- cycle
- self loop
- directed graph
- simple digraph
- non-directed graph
- unconnected graph
- strongly connected graph
- Directed acyclic graph
- Ways to represent a graph
- articulation points
- Edges
- Vertex
- spanning trees
The definition of a graph:
\(G=(E,V)\)
So a graph is a set of pairs of edges and vertices. Time complexity for traversing a graph depends on the method you use. In this case it is O(n2) because we are representing the graph on a matrix. If we would use a linked list to represent it, it would take O(n).
3.2. traversing a non cyclic graph with bfs
- Visiting Visiting in this case means print the value.
- Exploring This means, visit all the adjacent nodes.
Below we have a simple undirected graph with its adjacent matrix table representation:
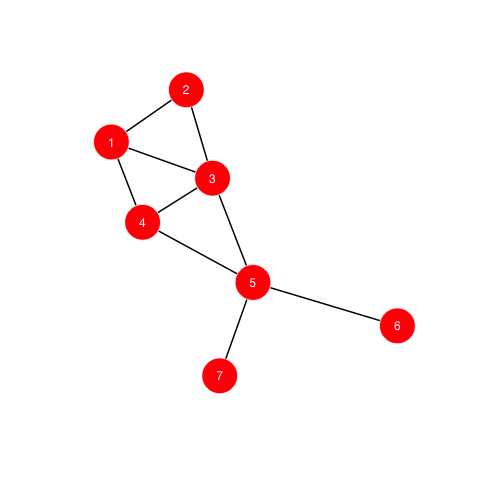
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
#include "stdio.h" #include "queue" #include "stdlib.h" #define N 8 using namespace std; void bfs(int firstElement); int main(int argc, char *argv[]) { printf("%s\n", "bfs with node: "); for (int i = 1; i < N; ++i) { printf("%d -> ", i); bfs(i); printf("\n"); } return 0; } void bfs(int firstElement) { int * visited = (int *) malloc(sizeof(int) * N); queue<int> q; // initialize visited array for (int i = 0; i < N; i++) visited[i] = 0; // visit printf("%d ", firstElement); // mark as visited visited[firstElement] = 1; // push to the queue q.push(firstElement); // repeat above process while (!q.empty()) { int r = q.front(); q.pop(); for (int c = 1; c < N; c++) if (gam[r][c] == 1 && visited[c] == 0) { printf("%d ", c); q.push(c); visited[c] = 1; } } free(visited); } // Note: gam is the graph-adjacent-matrix // the variable is loaded from the table displayed above
bfs with node: 1 -> 1 2 3 4 5 6 7 2 -> 2 1 3 4 5 6 7 3 -> 3 1 2 4 5 6 7 4 -> 4 1 3 5 2 6 7 5 -> 5 3 4 6 7 1 2 6 -> 6 5 3 4 7 1 2 7 -> 7 5 3 4 6 1 2
3.3. DONE traversing non cyclic graph with dfs
#include <cstdio> #include<stdio.h> #include "stdlib.h" #include "stack" #define N 8 void dfs(int firstNode); void recursive_dfs(int firstNode); int *visited_nodes = (int *)malloc(sizeof(int) * N); void clear_visited_nodes_array(void); int main(int argc, char *argv[]) { // initialize global array for (int i = 0; i < N; ++i) visited_nodes[i] = 0; for (int i = 1; i < N; ++i) { printf("dfs for node: %d -> ", i); recursive_dfs(i); printf("\n"); clear_visited_nodes_array(); } return 0; } void clear_visited_nodes_array() { for (int i = 0; i < N; ++i) visited_nodes[i] = 0; } void dfs(int firstElement) { // visit // explore int * visited = (int *) malloc(sizeof(int) * N); for (int i = 0; i < N; ++i) visited[i] = 0; std::stack<int> stack; // exploring stack.push(firstElement); while (!stack.empty()) { int e = stack.top(); stack.pop(); if (visited[e]) continue; printf("%d ", e); visited[e] = 1; for (int c = 1; c < N; c++) if (gam[e][c] == 1) stack.push(c); } } void recursive_dfs(int node) { if (visited_nodes[node] == 0) { printf("%d ", node); visited_nodes[node] = 1; for (int i = 1; i < N; ++i) if (gam[node][i] == 1 && visited_nodes[i] == 0) recursive_dfs(i); } }
dfs for node: 1 -> 1 2 3 4 5 6 7 dfs for node: 2 -> 2 1 3 4 5 6 7 dfs for node: 3 -> 3 1 2 4 5 6 7 dfs for node: 4 -> 4 1 2 3 5 6 7 dfs for node: 5 -> 5 3 1 2 4 6 7 dfs for node: 6 -> 6 5 3 1 2 4 7 dfs for node: 7 -> 7 5 3 1 2 4 6
3.4. Spanning trees
3.5. References
Some useful links that I used to build this entry.